Stairways to heaven: hiperbolički prostori M.C. Eschera
/ 26.08.2008. u 16:55
Euklidska geometrija je u filozofskim i metafizičkim diskusijama vekovima navodjena kao primer savršene organizacije ljudskog mišljenja i njegove rigorozne formalizacije. Zasnovana na definicijama osnovnih objekata i pet aksioma, ili postulata, ona je pokazala kako se sve druge tvrdnje i teoreme geometrije mogu iz ovih formalno-logički izvesti. Rečju, Euklidska geometrija je navodjena kao ideal ljudske racionalnosti, destilovano razumevanje prostornih dimenzija i odnosa, a vrhunac i cilj svake naučne teorije bi trebao da bude njena finalna aksiomatizacija po uzoru na geometriju. (Ovo je postignuto u klasičnim disciplinama fizike - mehanika, termodinamika, elektrodinamika, itd., se mogu na ovaj način formulisati).
Mi osnovne geometrijske pojmove - tačka, prava, ravan i njihove odnose - predajemo djacima u osnovnoj školi, jer su ovi koncepti intuitivno jasni čak i deci koja su tek početnički pismena. Peti Euklidov postulat, na primer, kaže da, ako u ravni imamo pravu P, i tačku A van nje, onda se kroz tu tačku A može konstruisati samo jedna prava koja je sa pravom P paralelna. Ovo je intuitivno jasno i osnovcima.
Ili, kao drugi primer, tvrdnja da je najkraće rastojanje izmedju dve tačke prava linija se intuitivno razume kao "ako treba da predjem put odavde do tamo, onda mi je najkraće da idem pravo''.
Medjutim, upravo je Peti Euklidov postulat vekovima bio predmet preispitivanja (svi su izgledi da ni sam Euklid nije bio njime zadovoljan) jer se smatralo da je on tvrdnja koja se može iz ostala četiri postulata izvesti kao teorema i nije ga potrebno postavljati kao aksiom. Tek je tokom XIX veka pokazano da ovo nije tačno - Peti postulat je nezavistan od ostala četiri, i mi, barem formalno-logički gledano, imamo slobodu da ga formulišemo kako želimo. U tom smislu postoje tri mogućnosti: ako imamo pravu P, i tačku A van nje, onda se kroz tačku A može konstruisati:
1.) Samo jedna prava koja je sa pravom P paralelna
2.) Nijedna prava koja je sa pravom P paralelna, ili
3.) Više pravih (beskonačno mnogo njih, zapravo) koje su sa pravom P paralelne
Svaka od ovih opcija nam daje nezavistan aksiomatski sistem sa svim formalno-logičkim posledicama i teoremama koje unutar njega slede. Prva opcija nam daje standardnu Euklidsku geometriju, dok nam druge dve daju ne-Euklidske geometrije. Konkretno, druga opcija daje eliptičku geometriju (još zvanu i Riemannova geometrija), dok treća daje hiperboličku geometriju.
Sematski, ovo je pokazano na donjoj slici:

Istorijski, otkriće ne-Euklidskih geometrija je predstavljalo revoluciju u matematici, a konkretne zasluge nekolicine matematičara u njihovom radjanju su i danas predmet preispitivanja. Konkretno, hiperbolička geometrija se još zove i geometrija Lobačevskog, ali i Lobačevski-Boljai geometrija, ili još, Lobačevski-Boljai-Gausova geometrija, po imenima ljudi koji su je otkrili. Kao i u svakom trileru, u ovoj priči ima zaturenih pisama, pitanja ''ko je za šta znao u vreme kad je ovaj drugi već...'', itd.
U svakom slučaju, otkriće ne-Euklidskih geometrija je predstavljalo pobedu logike i formalnog mišljenja nad svakodnevnom intuicijom.
Revolucija koja je ovim u matematici napravljena je, u velikoj meri, slična revoluciji u fizici, koja je nastala otkrićem teorije relativnosti i kvantne mehanike nekih 75 godina kasnije. I ona se proširila van matematike na druge oblasti ljudskog mišljenja i aktivnosti. Svet više nije onakav kakav je nekad bio, i stvari nisu onakve kakve nam na prvi pogled izgledaju.. U ''Romanu o Londonu'', na primer, glavni junak, ruski knez Rjepnin, se divi hrabrosti Nikolaja Ivanoviča Lobačevskog koji je smogao snage da posumnja u gvozdenu logiku dvehiljadugodišnje euklidske dogme, i suprotstavi se elementarnoj ljudskoj intuiciji.
Sledeće pitanje se odmah nameće: ako nam je Euklidska geometrija formalno i intuitivno jasna jer opisuje odnose u prostoru koji vidimo oko nas, kako izgledaju realne, prostorne, realizacije ne-Euklidskih geometrija? Kakvi su to prostori u kojima kroz tačku van date prave P ne možemo da konstuišemo ni jednu pravu (ili možemo više njih) paralelnu sa našom pravom P?
Odgovor na ovo pitanje, u slučaju eliptičke geometrije, je relativno lak i intuitivan, a u slučaju hiperboličke geometrije nešto teži. U oba slučaja, medjutim, da bi odgovorili, moramo da se vratimo na našu definiciju prave linije.
Podjimo od toga da je ‘'linija'' geometrijska putanja kojom je rastojanje izmedju dve tačke najkraće. U slučaju da se nalazimo u ravni, i te dve tačke se nalaze u toj ravni, onda je najkraća putanja izmedju njih upravo prava linija. Zamislimo, medjutim, da se, umesto u ravni, nalazimo na površini kugle, kao što je Zemljina lopta, na primer. Na takvoj površi nema pravih linija, ali ima najkraćih rastojanja. Konkretno, zamislimo neko selo u Indoneziji, tačno na ekvatoru, i drugo selo u državi Ekvador, takodje tačno na ekvatoru planete. Najkraće rastojanje izmedju ta dva mesta (tačke) se dobija putanjom koja ide upravo duž ekvatora. Sve druge putanje izmedju ta dva mesta, idući površinom Zemlje, su duže.
Ekvatorijalna linija na Zemlji je primer tzv. velikog kruga - to je onaj krug opisan oko sfere ciji se centar poklapa sa centrom sfere. Takvih velikih krugova oko sfere moze da se konstruiše beskonačno mnogo. Ako posmatramo bilo koje dve tačke na sferi, uvek je moguće konstruisati veliki krug koji te dve tačke sadrži, i ova konstrukcija je jednoznačna; kao i sa pravom linijom izmedju dve tačke u ravni, tako i dva velika kruga koja sadrže dve iste (nesuprotne) tačke se poklapaju. (Dve prave u ravni koje imaju više nego jednu zajedničku tačku se poklapaju. Dva velika kruga koja imaju više nego jednu zajedničku tačku, pod uslovom da tačke nisu sa suprotnih strana sfere, se poklapaju.) Najkraće rastojanje izmedju dve tačke na sferi je, dakle, takva putanja koja je deo velikog kruga konstruisanog kroz te dve tačke. Ukratko, ono sto je ‘'linija'' u ravni, to je na sferi veliki krug. U opštem slučaju, na nekoj površi, putanja najkraćeg rastojanja se zove geodezik.
Zamislimo sada veliki krug na sferi, ekvatorijalni krug na Zemlji, recimo, i neku tačku van njega (na primer, na poziciji Beograda na zemaljskoj kugli). Bilo koji veliki krug koji sadrži tu tačku (Beograd) će negde preseći ekvatorijalni krug. Preciznije, preseći će ga na dva mesta, sa suprotnih strana sfere.

Bitno je, medjutim, sledeće: ako imamo na sferi veliki krug V, i tačku van njega A, onda nije moguće konstruisati ni jedan veliki krug koji sadrži tačku A, a koji ne seče krug V. Drugim rečima, dva velika kruga na sferi se ili seku (u dve tačke sa suprotnih strana), ili se poklapaju. Geometrija velikih krugova na sferi je konkretna prostorna realizacija eliptičke geometrije, tj., opcije broj 2 gore.
U ovoj geometriji, na primer, zbir uglova u trouglu na sferi nije jednak 180 stepeni, kao sto je to slucaj sa trouglovima u ravni, nego je veci. Donja slika ovo ilustruje
.jpg/350px-Triangles_(spherical_geometry).jpg)
dva ugla na ekvatoru su po 90 stepeni svaki, i treci ugao je 50 stepeni, sto zajedno daje 230.
Ovo je, razume se, posledica zakrivljenosti sferne površine. Zakrivljenost se izražava poluprečnikom krivine, ili prosto krivinom, koja je na sferi inverzno proporcionalna poluprečniku sfere, tj. ~1/R. Što je manja sfera, manji je njen poluprečnik R, pa je njena površina zakrivljenija. Kad se sfera povećava, poluprečnik raste, pa njena površina postaje sve manje zakrivljena (ravnija). Mi živimo na sferi poluprečnika od oko 6700km, što je veliko u odnosu na naše dimenzije, te nam površina nekog jezera, recimo, izgleda ravna. Zakrivljenost Zemlje na tako malim rastojanjima može, za praktične potrebe, da se zanemari. U graničnom procesu, kada poluprečnik sfere postaje beskonačan, i zakrivljenost postaje jednaka nuli, te dobijamo površ koja je geometrijski ekvivalentna ravni i odgovarajući geometrijski odnosi su isti kao u Euklidskoj geometriji.
Zbog pozitivne zakrivljehosti sfere, kad idemo po njoj, horizont se ''gubi'' ispred nas ( nekad se kaže da se prostor ''smanjuje'') jer se površina kojom se krećemo savija ka centru sfere.
Postoje, medjutim, površine koji imaju negativnu zakrivljenost, kad se prostor ‘'povećava'' kako se krećemo ka horizontu. Fizička realizacija takvih prostora je realizacija hiperboličke geometrije. Zanimljivo je da fizički modeli ovakvih prostora mogu da se predstavle pletenjem! Konkretno dole je naštrikan, pomalo grub, fizički model hiperboličke ravni

Idući od sredine ka ivici, obod postaje sve veći (mora sve vise da se strika), kao da imamo sve više i više prostora. U prirodi se ovakve geometrije cesto pojavljuju.

Ovo gore je puz, a slicna geometrija se cesto vidi i na koralnim grebenima.
Geometrijskih (matematickih) reprezentacija hiperbolickog prostora ima nekoliko - od ''sedla'' do poluravni, a ja cu detaljnije opisati Poincareovu konstrukciju, poznatu kao Poincare disk model. To je prosto nacin da se gornji oblik predstavi u malo preciznije definisanom smislu od strikanja i hekleraja.
Model se sastoji od kruga jedinicnog poluprecnika, i tacaka unutar kruga, iskljucujuci obodne tacke. Beskonacna linija u toj geometriji je predstavljena ovako:

( Beskonacna je zato sto ide od jedne beskrajno udaljene tacke na obodu do druge takve tacke).
Ovaj luk izmedju dve krajnje tacke (''linija'') se dobija tako sto se konstruise ortogonalan krug na nas pocetni, a koji sadrzi obodne tacke izmedju kojih treba povuci liniju. Lucni odrezak tog kruga je linija koja nama treba. Taj luk je, u ovoj geometriji, najkrace rastojanje izmedju krajnjih tacaka. Otrogonalan krug, setimo se, je onaj krug koji sa nasim postojecim krugom u tackama preseka pravi ugao od 90 stepeni. Prema konstrukciji, dakle, sve linije u ovom modelu se seku sa obodom kruga pod uglom od 90 stepeni.
Drugu liniju, m, koja se sa ovom prvom ne sece, konstruisemo na slican nacin i dobijemo

Linije l je paralelna (ne sece se), sa linijom m. Jasno je da paralelnih linija sa linijom l ima beskonacno mnogo. Na primer, na donjoj slici je predstavljen jedan skup linija koje su paralelne sa datom linijom (oznacenom plavom bojom)

Trouglovi u hipebolickoj geometriji uvek imaju zbir uglova koji je manji od 180 stepeni, a idealan trougao je onaj ciji je zbir uglova jednak nuli.
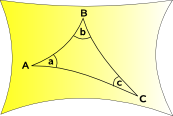
Ovo deluje pomalo bizarno, ali upravo to je logicna posledica aksioma sa kojima smo poceli. Pitagorina teorema za ovakve trouglove ne vazi u standardnom obliku, itd.
Sada. kad smo definisali sve tri geometrije, makar u najgrubljim crtama, mozemo da se posvetimo Escheru i njegovoj umetnosti.
Najprostiji nacin da to uradimo je da posmatramo ravan u nekoj od gornjih geometrija i da pokusamo da je poplocamo, ili ''naselimo'' nekom regularnom strukturom. Tako cemo da vidimo kakve su globalne posledice geometrija o kojima je rec. Tehnicki izraz za podelu prostora na poligone je teselacija.
Euklidsku ravan, na primer, koja je kao pod u kuhinji, mozemo da poplocamo plocicama regularnog oblika kao sto su

Ovde imamo regularne trouglove, cetvorouglove, sestouglove. Sest trouglova se srecu u jednoj tacki i idealno pasuju jer im se uglovi, od 60 stepeni, sabiraju do punog kruga (360 stepeni); slicno je sa cetiri kvadrata i njihovim uglovima od 90 stepeni, i tri sestougla i uglovima od 120 stepeni. A sta je sa petouglovima, osmouglovima, i drugim pravilnim poligonima? (Sedmougao smo preskocili, on se ne moze konstruisati lenjirom i sestarom). Pa, ako bi pokusali sa petouglovima, dobili bi nesto ovako

Posto je ugao izmedju stranica petougla 108 stepeni, a tri se takva petougla srecu u jednoj tacki, nedostaje nam 360-3*108=36 stepeni da popunimo prostor. Kao da je euklidska ravan suvise ''velika'' da se poploca pentagonima. Nedostaje nam 36 stepeni. Sa osmouglovima (i mnogouglovima veceg reda) situacija je obrnuta - ugao izmedju stranica osmougla je 135 stepeni, pa ako se tri osmougla sretnu u jednoj tacki 3*135=405 stepeni, tj. prebacili smo pun krug za 45 stepeni. Euklidska ravan je suvise ''mala'' da popunimo prostor osmouglovima. Situacija je jos gora sa poligonima viseg reda.
Za one koji vole matematiku, sledeci rezultat moze da se izvede na elementaran nacin. [Rotacije za ugao t, koje ostavljaju poplocanost invarijantnom moraju da zadovoljavaju uslov cos(t)= (m+n)/2, gde su m i n celi brojevi. Kosinus ugla, dakle, moze da bude ceo broj ili polovina celog broja, tj., da bude jednak -1, -1/2, 0, +1/2 i 1. Ovo odgovara uglovima od 180, 120, 90, 30 i 0 stepeni, dakle osama rotacije drugog (360/180), treceg (360/120), cetvrtog (360/90) i sestog (360/30) reda.]
Escher je ovo koristio u svojim slikama kao na primer ravan poplocanu elementima sa osom rotacije 4 reda:

Kako ovo poplocavanje izgleda na eliptickoj ravni (sferi)? Najocevidniji primer je ovaj:

Kad bi loptu hteli da poplocamo sestouglovima, to ne bi mogli - sestouglovi pokrivaju euklidsku ravan, i sfera je suvise ''mala'' za sestouglove. Ali, setimo se da nam petouglovi ne pokrivaju euklidsku ravan (ravan je suvise ''velika'' za petouglove). Pogodnom kombinacijom petouglova i sestouglova, visak jednog prostora i manjak drugog se tacno kompenzuju da mozemo da napravimo fudbalsku loptu, kao sto svaki fudbaler zna.
Kako se poplocava hiperbolicka ravan?
Poincare je konstruisao regularnu petougaonu teselaciju hiperbolicke ravni i ona izgleda ovako:

Sve ove linije se uzajamno seku pod uglom od 90 stepeni. Kako idemo ka obodu kruga, plocice postaju sve manje. Ako zamislimo da se i mi u istoj proporciji smanjujemo, potrebno je beskrajno dugo da idemo da bi stigli do oboda. (I u Euklidovoj ravni nam je potrebno beskrajno dugo da idemo da bi stigli do kraja beskonacne linije.) Koristeci ovo pravilo, Escher je napravio ovakvu reprezentaciju - cuveni Kruzni limit 3

Tu je i popravio neke nedostatke koji su bili kritikovani u ranijem radu. Sve ribe iste boje duz jedne linije se krecu u istom pravcu, i ovo je prvi hiperbolicki motiv ikad napravljen koji sadrzi savrsenu cetvorobojnu simetriju.
Najzad, mozemo da se zapitamo kako izgleda visedimenzioni hiperbolicki prostor?.
Na donjoj slici je prikazana teselacija hiperbolickog prostora pomocu dodekaedara

Skorije je pokazano da ovakve strukture potpuno i regularno popunjavaju hiperbolicki prostor.
Medjutim, ovo nije samo vezba iz geometrije. Nas zanima, recimo, kako «izgleda» kosmos na globalnoj skali. Da li je na globalnoj skali prostor u kome postojimo hiperbolican, eliptican ili ravan?
Na ovo pitanje je za sada tesko odgovoriti zbog nedostatka podataka. Merenjem pozadinskog zracenja (WMAP) ustanovljena je anizotropija kosmosa predstavljana donjom slikom (ovo nije oblik kosmosa vec samo reprezentacija njegove anizotropije)
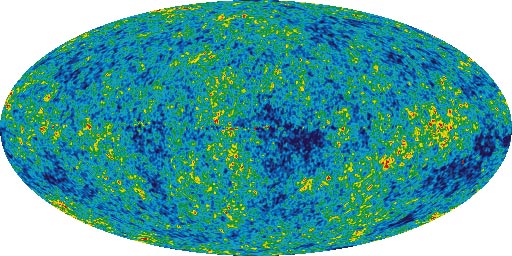
Kosmos se sastoji od toplijih i hladnijih regiona, medjutim na vecim skalama ove se varijacije izjednacavaju i gube i dobije se globalna izotropija. Jedno objasnjenje za ovu pojavu je da je kosmos relativno mali. Ovo je za sada samo spekulacija, ali ako se nas prostor «savija» u sebe na neki nacin, onda moze da se desi da WMAP merenjima stalno vidimo jedan te isti deo prostora vise puta ponovljen, kao u kuci ogledala. Ako zaista zivimo u takvom prostoru, to bi bilo kao kada bi iz sobe, koja ima dvoja vrata, izasli kroz vrata na jednoj strani i time automatski krocili u istu sobu kroz druga vrata, na suprotnom zidu.

Za sada, ovo je samo jedna mogucnost, koja nije bas svima do kraja jasna, ali Escher bi je svakako razumeo.
Blogovi autora
- Kako je nastao krug dvojke? (396)
- Riznica igara (160)
- Under the volcano – izbori na Martiniku 1902. (161)
- Nobelova nagrada iz fizike za 2021. godinu (364)
- Fala Kurzu! (175)
- Vlaho (1855-1922) (117)
- Пропис или опис, питање је сад? (271)
- Умро је друг Тито! (1114)
- Ове улице знају моје кораке... (509)
- Under the volcano – izbori na Martiniku 1902. (96)
- John Horton Conway (26.12. 1937 – 11.04.2020) (156)
- Plus ça change plus c'est la même chose (367)
- 2020 (663)
- Грофовска књижевност – покушај једног упита (28)
- Vlada Petrić 1928-2019 (52)
- Hiroshima mon amour (507)
- Dark Lady (110)
- Kolacova pretpostavka (167)
- Big, really BIG (152)
- Filmičan (332)
Najnovije VIP blogeri
- "Ribnikar" je mrtav
angie01 - амалгамацијом списатељства
Черевићан - Amalipe
angie01 - Izgrebani Oklop
Spiridon - Razonoda
njanja_de.manccini - Javna rasprava o Beogradskom sajmu i Generalštabu
Đorđe Bobić - Gde je krenuo Saban
natasa_tasic_10 - Davimo Beograd iliti DB
Ivan Blagojevic - Oda Drustvenim Naukama
Spiridon - OTVORENO PISMO MINISTARSTVU ZDRAVLJA
razmisljam
Najnovije blogeri
- DUB PUB: Bilo je to davno...
docsumann - Дежуловић за сиромашне
omega68 - DUB PUB: Everyday Is A War...for Tomorrow
docsumann - KRUNSKI DOKAZ ZA NEIZLAŽENJE NA "IZBORE"
Filip Mladenović - DUB PUB: Stepping Out From The System
docsumann - Majstor za ljuljaške, klackalice, tobogane i ... II DEO
Filip Mladenović - ŽUTA OSA (8/24)
horheakimov - DUB PUB: Milion kvadrata
docsumann - Dokon um đavolje igralište
zilikaka - НАЦРТ РЕЗОЛУЦИЈЕ О ГЕНОЦИДУ У СРЕБРЕНИЦИ
Filip Mladenović
Arhiva
Kategorije aktivne u poslednjih 7 dana
- Muzika (3)
- Eksperimenti u blogovanju (2)
- Zabava (2)
- Hobi (2)
- In memoriam (1)
- Sport (1)
- Astronomija (1)
- Životni stil (1)
- Astrologija (1)

