Fraktalna privlačnost

Klasična geometrija je nastala iz praktičnih znanja stečenih premeravanjem zemljišta za potrebe gradjevine, navigacije, itd. Danas je ona poznata kao Euklidova geometrija - matematička disciplina koja se bavi dužinama, uglovima, rastojanjima, površinama i drugim prostornim odnosima.

U svom delu "Elementi", Euklid prvo definiše osnovne geometrijske elemente kao što su tačka, prava i ravan: tačka zauzima nula dimenzija u prostoru, prava jednu, a ravan dve dimenzije. Kombinacijom elementarnih se zatim dobijaju složenije geometrijske figure: trouglovi i mnogouglovi (u ravni), kao i kocke, piramide, valjci, kupe, itd. Medjutim, ako pogledamo prirodne tvorevine koje nas na Zemlji okružuju, one nisu nikad, ili skoro nikad, pravilnog geometrijskog oblika. Obale mora i jezera, planine, rečna korita, oblaci, drveće i slično, imaju nepravilne oblike koji se, naizgled, ne mogu opisati prostom euklidskom geometrijom; ili barem ne na jednostavan način. Rečju, Euklidova geometrija kao da nije geometrija prirodnih oblika.

Ne tako davno, medjutim, ispostavilo se da postoji klasa drugih geometrijskih elemenata, koji su pogodniji za opisivanje "neregularnih" oblika kakvi se nalaze u prirodi. Takvi elementi se pojavljuju kada se proučava dinamika kompleksnih sistema, haotično ponašanje ("teorija haosa" kako se još popularno zove) i slično, a zajednička osobina im je da po pravilu imaju "razlomljenu", necelobrojnu prostornu dimenziju, pa se kolektivno zovu "fraktali".

Fraktali, kakvi se vidjaju na slikama i posterima (i niže na ovom blogu), imaju prilično komplikovane oblike; medjutim, njihova konstrukcija je najčešće elementarna.

Evo primera.

Jedan od najprostijih fraktalnih elemenata, Koch-ova kriva, se konstruiše kao što je prikazano na slici.

Polazimo od osnovnog elementa (inicijatora) - u ovom slučaju od linije dužine L=1, kao na vrhu slike. Zatim, uvedemo generator (osnovno pravilo transformacije): pravilo je ilustrovano na slici, a rečima ono glasi: podeli liniju na tri jednaka dela; srednji deo izbaci i zameni ga "šatorom" (onim šiljkom u sredini kako slika, generator, pokazuje). I to je sve, to je ceo princip.

Sada tu transformaciju primenimo rekurzivno na generator (dobijemo nivo 2), pa ponovo primenimo isto pravilo za svaki pravi odsečak na nivou 2, da dobijemo nivo 3, pa to isto ponovimo, i tako u beskrajon. Posle beskonačno mnogo rekurzivnih primena ove transformacije dobije se tzv. Koch-ova kriva. Naravno, sa svakim novim korakom, detalji na krivoj su sve sitniji i sitniji, ako osnovnu dužinu ostavimo da bude ista.

Da smo, umesto od odsečka linije (inicijator), počeli od trougla, na primer,

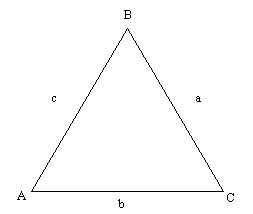i na svaku stranicu ovog trougla primenili gornju konstrukciju, dobili bi malo drugačiju Koch-ovu krivu kakva je prikazana na desnoj strani slike. Hej, pa ovo liči na pahuljicu!

Ali, pre nego što se suviše prepustimo radovanju, da malo detaljnije pogledamo ovu konstrukciju.

Prvo, sa svakom primenom transformacije, ukupna dužina krive se povećava za faktor (4/3), kao što se vidi na slici (prosto, po ovom pravilu mi jedan segment dužine 1/3 zamenimo sa dva segmenta od 1/3). Posle N primena ove transformacije dužina krive je (4/3) na N-ti stepen, tj. (4/3)^N, zato što se sa svakom primenjenom transformacijom dužina krive povećava za ovaj faktor. Za veliko N, broj (4/3)^N postaje proizvoljno veliki. Mi smo, dakle, ovim postupkom, od linije dužine = 1 napravili liniju dužine = beskonačno.

Drugo, lako se može pokazati da je površina ispod Koch-ove krive strogo manja od 3/2, tj. da ima konačnu vrednost. Ukratko, konstruisali smo geometrijski objekat koji ima konačnu površinu a beskonačan obim.

Treće, počeli smo od linije konačne dužine, a došli smo do krive beskonačne dužine. Linija od koje smo počeli, kaže nam Euklid, ima dimenzionalnost d=1. To jest, ona zauzima jednu prostornu dimenziju ("dužina bez širine", kaže Euklid). Kolika je dimenzionalnost Koch-ove krive? Na ovo pitanje može da se odgovori u dva tango koraka.

Počnimo opet od one prave linije dužine 1. Zamislimo da je podelimo na tri jednaka dela (motiva), tako da je svaki deo dugačak 1/3. Originalna "količina" linije (=1) se dobije tako što tri dela (3) pomožimo sa veličinom motiva (1/3), tj. 3*1/3 = 1. Zamislimo sada da smo počeli od kvadrata površine = 1, i svaku stranicu podelili, na isti način kao i gore, na tri dela i išpartali ga kao na djačkim sveskama. Dobili bi 9 malih kvadrata unutar onog početnog. Površinu originalnog kvadrata (=1) dobijemo tako što 9 motiva (kvadratića) pomnožimo sa veličinom kvadratića (1/3)^2, to jest 9*(1/3)^2=1, opet. Da smo to isto uradili sa kockom zapremine = 1, podelili je ravnima, dobili bi 27 kockica i originalnu veličinu kocke (=1) bi dobili tako što bi 27 elemenata pomnožili veličinom "motiva", tj. 27*(1/3)^3=1. Ha! U slučaju linije množimo sa (1/3), u slučaju ravni sa (1/3)^2, u slučaju kocke (1/3)^3. Ovaj stepen (1,2, ili 3) na koji se mora podići veličina motiva (1/3) se, dakle, može definisati kao dimenzija objekta koji posmatramo (linija, kvadrat, kocka). Ovo je pomalo "uvrnut" način da se definiše dimenzija, ali baš ovo je definicija tzv. Hausdorfove dimenzije nekog objekta, za razliku od Euklidove (još znane i kao topološke) dimenzije. Prema ovoj definiciji, dakle, i Euklidova i Hausdorfova dimenzija naše početne linije je =1. Pa to je isto. Jaka stvar! Ovo je bio prvi korak.

Pogledajmo sada Koch-ovu krivu. Onaj generator gore na slici ima 4 motiva, svaki dužine (1/3). Kako ćemo iz toga dobiti originalnu veličinu 1? Um, hum, znači nama treba da pomnožimo 4 sa (1/3)^(neki stepen) da bi dobili 1? Da, i taj stepen se lako izračuna iz jednačine 4*(1/3)^d=1, to jest d=log(4)/log(3)=1.2619... Ali, zar nije Koch-ova kriva još uvek "dužina bez širine"? Jeste, i njena topološka (Euklidska) dimenzija je =1. Njena Hausdorfova (tehnički, Hausdorf-Besicovitch) dimenzija je = 1.2619.

Geometrijski objekat čija je Hausdorfova dimenzija veća od njegove Euklidske dimenzije se zove fraktal - ovo je definicija sa kojom sam mogao da počnem ovaj blog, ali onda me neki ne bi razumeli. Sada svi razumeju. To je bio drugi korak.

Koch-ova kriva je fraktal. Dimenzionalno, ona nije ni prava (d=1) ni ravan (d=2) već nešto izmedju.

Umesto one konstrukcije gore koja nam je dala Koch-ovu krivu, mogli smo da uradimo drugačije. Počnemo opet od linije dužine =1, podelimo je na tri jednaka dela, i srednji deo prošto izbacimo kao na slici dole (linija je podebljano nacrtana da bi se bolje video postupak). Pa to, sa onim što nam je ostalo, ponovimo, pa ponovimo, itd. Na kraju dobijemo jedan "tačkast" objekat koji se zove Kantorov skup (ili Kantorova prašina, ponekad). Dimenzija ovog skupa? Pa, pošto sada imamo dva motiva (2), svaki dužine 1/3, treba da rešimo 2*(1/3)^d=1 što daje d=log(2)/log(3)=0.6309.., tačno duplo manje nego Koch-ova kriva. Kantorov skup je fraktal. Nije ni tačka (d=0) ni prava (d=1) već nešto izmedju.

Možemo sada da se igramo sa ovim konstrukcijama primenjujući ih na razne "obične" objekte.

Recimo, uzmemo kvadrat, izdelimo ga na 9 jednakih kvadratića, pa izbacimo srednji, pa to ponovimo, i ponovimo, itd., dobijemo:

Sierpinski-jev "tepih". Dimenzija? Kad izbacimo jedan kvadrat, po konstrukciji, ostane nam 8, svaki sa stranicom 1/3, dakle 8*(1/3)^d=1, ili d=log(8)/log(3)=1.8928.

Da smo počeli od kocke i napravili sličnu konstrukciju, dobili bi Mengerov "sundjer"

Dimenzija? Po konstrukciji, od 27 malih kockica, srednje se odbacuju, tako da ih ostane 20. Znači 20*(1/3)^d=1, što daje d=2.72683.

Fraktal može i "konstruktivno" da se napravi. Umesto izbacivanja delova, možemo da pojemo od prostog elementa, vertikalne linije (stable), na primer, i da joj na jednom kraju dodamo dve grane, pa opet na krajevima grana dve grane, itd. , da dobijemo fraktalno drvo:

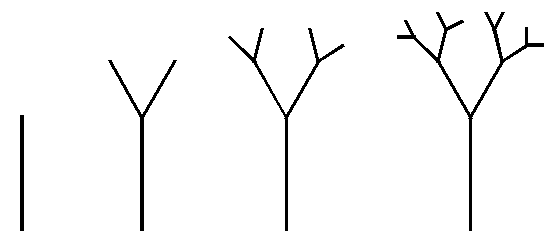
Ovim načinom je moguće napraviti na desetine i stotine različitih fraktala. I to je sve?! To su fraktali? Male geometrijske igrice sa lepim sličicama?

Nije sve.

Prvo, ovakvim načinom možemo da konstruišemo niz objekata koji veoma "liče" na nepravilne objekte u prirodi. Drugo, dimenzionalnost ovih objekata je bliža onoj koja se sreće u prirodi - prirodni odjekti imaju razlomljenu dimenzionalnost koja se može izmeriti. Konkretno, obala Britanije:

ima dimenziju d=1.24 (manja od Koch-ove krive),

Obala Norveške:

ima dimenziju 1.52

Karfiol:

ima dimenziju 2.33

Dok površina ljudskog mozga:

ima dimenziju 2.79.

Sve ovo ukazuje da prirodni procesi rasta i optimalne adaptacije spoljašnjim uslovima proivode oblike koji su fraktalni. Mozak, na primer pokušava da ima što je veću moguću površinu, sa što manjom zapreminom (zbog problema kao što su veličina glave deteta i porodjaj), pa je to "rešio" tako što je površinu "izvijugao" i "zgužvao" da bi bila veća. (Kao u onom vicu: "Švajcarska je najveća zemlja na svetu, samo što je malo zgužvana"). Ljudski mozak je "zgužvniji" od karfiola!

Fraktal se, kao što vidimo, formira rekurzivnim procesom. Ova operacija može da se predstavi običnom funkcijom. Jedna od najprostijih funkcija ove vrste je f(n+1)=f(n)^2+c, gde je c neki (kompleksan) broj, a f(n) prethodna vrednost funkcije f.

Dakle: f(1)=f(0)^2+c; f(2)=f(1)^2+c, itd. f(0) se zove "seed", ili "seme", c je broj.Ako nacrtamo skup svih onih vrednosti brojeva "c" za koji ova iteracija NE ode u beskonačnost, dobicemo čuveni Mandelbrotov skup, koji može da se vidi na stotinama postera, a koji izgleda ovako:

Na horizontalnoj osi je realan deo broja c, na vertikalnoj je imaginaran. Ovaj naizgled neobičan objekat postaje zanimljiviji kad ga pogledamo malo bliže. Nalazimo se u svemirskom brodu i krecemo:

w=4 w=0.8 w=0.16

w=0.032	w=0.064	w=0.00128

w=0.000256 w=000512 w=0.00001024

Na slikama gore se nalazi isti objekat (Mandelbrotov skup), samo na sve detaljnijim i detaljnijim skalama.

Broj w pokazuje širinu slike. Polazimo od w=4, a upolovljavanjem dolazimo do smanjenja za 0.00000001*2^10. Na poslednjem nivou vidimo originalnu sliku ponovo.

Unutar ovog skupa postoje, kao što se vidi, sve manje i kompleksnije structure, nalik na poseban kosmos. Postoje "ostrva" i "mora" i ponovo ostrva, i tako beskrajno, ostrva i mora i ostrva. Ovo poslednje sjajno ostrvo je kopija prvog, i unutar njega postoji struktura kakvu mo vec videli, i tako dalje, i tako dalje.

Na jednom mestu, u svojoj knjizi "Emperor's New Mind", Penrose razmatra ovaj skup I ovakve slike i pita se: "Da li je ovaj kosmos inherentna priroda matematike, ili je to samo u nasoj svesti? " I odgovara: "Ja sam Platonista. Ove ideje postoje, nezavisno od toga da li smo ih mi ljudi svesni ili nismo".

Jos jedan vazan dodatak: mnogi matematicari su davno znali za postojanje ovakvih struktura. Medjutim, bez kompjutera kakve dana ima svaka kuca, oni nisu mogli da crtaju ovakve slike. Kompjuteri su nasem zivotu dodali prozor i svet za o kome ranije nismo znali skoro nista.

A u svakodnevnom zivotu: kad sledeci put budete kupovali Svajcarski sir u radnji, pitajte prodavca kolika je fraktalna dimenzija to supljikavog objekta. Nema smisla da vam prodaje supljine po skupoj ceni.

Po mom mišljenju, u ovome se sastoji neodoljiva fraktalna privlačnost. Fractal attraction.

P.S.

U sledećem nastavku će biti reči o fraktalima i haosu. Ovde prosto nije bilo mesta da za sve.