Najteži problem na svetu I: Poincare-ova pretpostavka
/ 15.06.2008. u 15:04

Clay matematički Institut je privatna organizacija posvećena širenju i popularizaciji matematike. Izmedju ostalih delatnosti, Clay institut pruža podršku nadarenim matematičarima i finansira istraživanja izuzetno talentovanih matematičara. U široj javnosti je ovaj Institut još poznat i po svom spisku Milenijumskih matematičkih problema, za čije rešenje je ponudjena nagrada. Dakle, onaj ko uspe da reši neki problem sa tog spiska dobija nagradu Instituta u iznosu od 1 milion dolara.
Medju Milenijumskim problemima nalaze se (ili su se nalazili) problemi postavljeni pre više stotina godina, ali i oni postavljeni poslednjih decenija - svi oni se svrstavaju medju najteže matematičke probleme na svetu. Neki su strogo matematičke prirode, dok neki spadaju medju nerešene probleme u matematičkoj fizici (mass gap u Yang-Millsovoj teoriji polja, na primer).
Od najpoznatijih problema sa Milenijumskog spiska treba pomenuti Veliki Fermat -ov problem, koji je rešio A. Wiles 1996. godine, a postavio ga P. Fermat oko 350 godina ranije. Postavka ovog problema, sama po sebi, je elementarna:
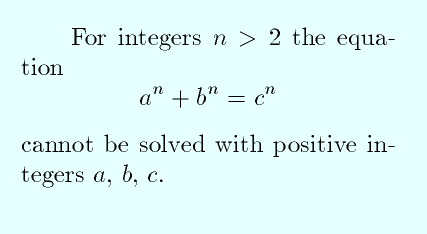
(Za bilo koji ceo broj n veći od 2, ne postoje celi brojevi a, b, i c, za koje gornja jednačina ima rešenje.)
Dokaz ove tvrdnje je pronadjen tek posle cca 350 godina bezuspešnih pokušaja mnogih matematičara. Rešenje ovog problema, kao takvog, nije napravilo neki dramatičan proboj u matematici, ali je put koji je do rešenja doveo veoma značajan. Ključnu ulogu u Wiles - ovom rešenju igraju tzv. modularne eliptičke krive i njihove osobine, a eliptičke krive igraju ključnu ulogu u današnjoj kriptologiji. Kada preko kompjutera vršite transakcije sa vašom bankom, ili plaćate nešto, vaše poruke (broj računa, broj kartice, i slično) se šifruju, i na drugom kraju dešifruju, pomoću algoritma koji koristi eliptičke krive.
Još se dva "stara" čuvena matematička problema nalaze na Milenijumskom spisku: Poincare-ova pretpostavka (Poincare conjecture) i Riemann-ova hipoteza (Riemann hypothesis). Prvu je postavio Poincare 1904. godine, i ona je rešena 2003. godine.
Riemann-ova hipoteza, jož uvek nedokazana, je postavljena pre oko 150 godina i danas se smatra za najteži problem u matematici. Ona govori o stvarima koje su u samoj suštini brojeva i igra fundamentalnu ulogu u matematici. David Hilbert je jednom rekao: "Ako me neko oživi za 1000 godina, moje prvo pitanje će biti da li je dokazana Riemann-ova hipoteza".
O Riemann-ovoj hipotezi ću pisati u narednom nastavku, a ovaj blog je posvećen Poincare-ovoj pretpostavci i njenom rešenju.

Za Henri Poincare-a (1854-1912) se kaže da je bio polimat, jedan od poslednjih velikih univerzalista, koji je briljirao u skoro svim vodećim naučnim disciplinama svog vremena. Ključni su njegovi doprinosi u Teoriji Relativnosti (Poincare-ove grupe su fundamentalna matematička formulacija, objavljena tri meseca pre Ajnštajnovih radova u ovoj oblasti), nelinearnoj dinamici i teoriji haosa (Poincare-ov presek, Poincare preslikavanje), teoriji dinamičkih sistema (Poincare recurrences - o ovome sam malo pisao u tekstu o strelici vremena), i slično. Već samo ovaj kratak spisak ukazuje koliki je vizionar Poincare bio - mnogi od ovih problema su i danas, ceo vek kasnije, u fokusu istraživanja u fizici i matematici.
Poincare-ov doprinos u matematici je preobiman da bi se ovde detaljnije naveo, ali za potrebe ovog teksta dovoljno je reći da je on jedan od utemeljivača topologije, posebno algebarske topologije, kako se ova pod-grana danas zove. Poincare-ova pretpostavka se odnosi na topološke osobine prostora, i njen dokaz je tehnički izuzetno kompleksan - vodećim topolozima sveta je bilo potrebno par godina da "ispeglaju'' originalnu verziju dokaza koju je na internetu objavio Grigorij Perelman.
Ali, bez obzira što sve ovo gore izgleda kao apstraktna i egzotična matematika, ona ima jednostavan i sasvim konkretan značaj za osnovne predstave o prostoru-vremenu u kome mi, i kosmos, postojimo. Zbog toga je dokaz Poincare-ove pretpostavke, na naslovnoj stranici časopisa Science, najavljen kao naučno otkriće godine (poznajem mnoge matematičare koji smatraju da je ovo otkriće veka).
U ostatku ovog teksta ću pokušati da preciznije opišem značaj ovog otkrića, bez korišćenja komplikovanih matematičkih ili tehničkih izraza.
Topologija je grana matematike koja se bavi geometrijskim objektima i oblicima, ali, za razliku od geometrije, rastojanja i uglovi na takvim objektima u topologiji ne igraju značajnu ulogu. Konkretno, onaj niz objekata prikazan na slici sa početka ovog teksta i na slici ispod, je topološki ekvivalentan, tj., sa topoloske tačke gledišta svi ti predmeti su isti jer se mogu pomoću neprekidnih transformacija (razvlačenja, sabijanja i slično) modifikovati iz jednog oblika u drugi, od početnog oblika lopte, do onog poslednjeg prikazanog u nizu, "tučka za avan", da ga tako nazovemo.

Ako zamislimo da su gornji objekti napravljeni od plastelina, onda svaki mogući objekat koji možemo da napravimo gnječeći i razvlačeći taj plastelin, a da u njemu ne pravimo rupe, je topološki ekvivalentan osnovnom objektu, onoj crvenoj sferi (loptici) sa kojom smo počeli gore. Preciznije, ovde imamo u vidu površine tih objekata prikazanih gore - i te površine se mogu neprekidnim transformacijama, bez kidanja, dakle, modifikovati iz jedne u drugu, i, u konačnoj instanci, u površinu početne lopte. Površina te (trodimenzione) lopte je dvodimenzioni objekat koji se zove sfera, ili, u tehničkom žargonu, 2-sphere, da bi se istakla njena (dvo)dimenzionalnost. Površina 4-dimenzione lopte se zove 3-sphere, itd.
Pošto sfera ne sadrži "rupe" (broj rupa=0), ona se tehnički još zove i površ genusa 0.

Za razliku od ove sfere (2-sphere), površina torusa (djevreka) se označava kao površ genusa 1.

jer sadrži jednu rupu, dok se površina duplog torusa

označava kao površ genusa 2, jer ima dve rupe, itd.
Genus neke površi je takodje i topološka invarijanta te površi, tj., neprekidne transformacije te površi ne mogu promeniti njen genus. Ovo je samo tehnički izraz nečega što nam je intuitivno jasno: kako god deformisali (bez kidanja i pravljenja rupa) loptu plastelina sferne površi (genusa=0), dobićemo neki objekat čija je površ takodje bez rupa (genusa=0). Gnječenje i razvlačenje ne menja genus površi.
Dakle, sve lopte, kocke, kupe, piramide, itd., imaju površi koje su topoloski ekvivalentne jedna drugoj i jednake površi genusa 0.
Svi djevreci, šolje sa jednom drškom, krigle, čajnici, i slični predmeti sa jednom drškom, imaju površi koje su ekvivalentne jedna drugoj i jednake površi genusa 1. (Otuda potiče i poznata definicija da je topolog čovek koji ne razlikuje svoju kriglu od svog djevreka.)
Dobro, završili smo sa definicijama, sada prelazimo na suštinu.
Zamislimo sada neka dvo-dimenziona bića koja žive na nekoj površi odredjenog genusa. Konkretno, zamislimo mrava koji živi na površi lopte, ili djevreka. Preciznije bi bilo reći da taj mrav živi u površi, jer ne poseduje treću dimenziju (visinu), da se iznad te površi izdigne i da je sagleda.
OK, mrav u površi lopte ili djevreka. On može da se slobodno kreće u tom prostoru napred, nazad, levo, desno.
Pitanje, koje je postavio Poincare, glasi: može li taj mrav, krećući se po toj površi, da ustanovi na kakvoj površi živi? Da lokalnim merenjima utvrdi da li živi na lopti, ili djevreku, ili nečemu drugačijem?
Odgovor je - može.
Poincare je dao konkretan, mada ne i sasvim praktičan, način da se do ovog odgovora dodje.
Zamislimo da taj mrav podje od neke početne tačke A na toj površi, luta po svojoj površi kako želi, i sve vreme tokom tog lutanja za sobom otpušta nit konca, čiji je početak fiksiran u polaznoj tački A (nešto kao Arijadnina nit). Najzad, kad mu dosadi, odluči da se vrati nazad na početnu tačku A. Kad je stigao u početnu tačku, A, mrav počne da povlači onaj kraj niti koji sa sobom ima.
Ako mrav živi na sferi (površ genusa 0), onda će cela ta zatvorena petlja po kojoj se kretao, povlačenjem da kolabira u tačku. Proces je ilustrovan na slici dole

Početna tačka je tačka bele boje na ovoj sferi, a putanja mrava (nit) je je crna linija. Pošto je sfera površ genusa 0 (nema rupa), povlačenjem ta nit se redukuje i kolabira u tačku.
Da je mrav kojim slučajem živeo na površi djevreka, situacija bi bila drugačija, kao što prikazuje donja slika.
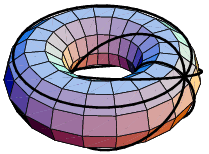
Crnim linijama su označene neke od mogućih putanja. Kao što vidimo, povlačenjem niti, ona neće kolabirati u tačku, zato sto je površ torusa površ genusa 1.
Pomoću svoje niti, kao mrežom, mrav je uspeo da uhvati rupu u svom prostoru. Kada živi na sferi, mreža ostane prazna.
I najzad, milenijumsko pitanje.
Mi postojimo u 3-dimenzionom prostoru. Kazemo da je svemir konačan, ali da nema ivica - pojam o mestu "van kosmosa" nema smisla (slično kao što je planeta na kojoj živimo konačna, ali nema ivica, tj., nema "kraja sveta", kako se to nekad zvalo).
Mi, dakle, živimo na 3-površi. Da li možemo, po analogiji sa ovim mravom gore, da utvrdimo da li naša 3-površ ima genus 0, 1, 2...? Da li je ekvivalentna sferi, ili djevreku, ili nečemu složenijem?
Poincare-ova pretpostavka kaže da možemo, ali on ovu pretpostavku nije uspeo da dokaže.
Sto godina kasnije, 2003. godine, pretpostavku je dokazao Grigorij Perelman. Novčanu nagradu od milion dolara za rešenje milenijumskog problema je odbio da primi, i otišao da sakuplja pečurke lutajući šumama oko St. Petersburga. Ne zna se da li za sobom pušta nit.
U praktičnom smislu, ovaj dokaz, za sada, nema neku posebnu primenu. Medjutim, njegova epistemološka vrednost je ogromna. Postojeći unutar jednog zatvorenog sistema (prostora u ovom slučaju), mi možemo, makar u principu, da odlučimo o nekim globalnim osobinama tog prostora, "ne izlazeci" iz njega. Zanimljivo je ovo uporediti sa Goedelovom teoremom o protivrecnosti.
Blogovi autora
- Kako je nastao krug dvojke? (396)
- Riznica igara (160)
- Under the volcano – izbori na Martiniku 1902. (161)
- Nobelova nagrada iz fizike za 2021. godinu (364)
- Fala Kurzu! (175)
- Vlaho (1855-1922) (117)
- Пропис или опис, питање је сад? (271)
- Умро је друг Тито! (1114)
- Ове улице знају моје кораке... (509)
- Under the volcano – izbori na Martiniku 1902. (96)
- John Horton Conway (26.12. 1937 – 11.04.2020) (156)
- Plus ça change plus c'est la même chose (367)
- 2020 (663)
- Грофовска књижевност – покушај једног упита (28)
- Vlada Petrić 1928-2019 (52)
- Hiroshima mon amour (507)
- Dark Lady (110)
- Kolacova pretpostavka (167)
- Big, really BIG (152)
- Filmičan (332)
Najnovije VIP blogeri
- Amalipe
angie01 - Izgrebani Oklop
Spiridon - Razonoda
njanja_de.manccini - Javna rasprava o Beogradskom sajmu i Generalštabu
Đorđe Bobić - Gde je krenuo Saban
natasa_tasic_10 - Davimo Beograd iliti DB
Ivan Blagojevic - Oda Drustvenim Naukama
Spiridon - OTVORENO PISMO MINISTARSTVU ZDRAVLJA
razmisljam - Dovidjenja, gospodine Bobicu!
angie01 - Klasicna tema- Beograd, popodne i gitare
jednarecfonmoi
Najnovije blogeri
- KRUNSKI DOKAZ ZA NEIZLAŽENJE NA "IZBORE"
Filip Mladenović - DUB PUB: Stepping Out From The System
docsumann - Majstor za ljuljaške, klackalice, tobogane i ... II DEO
Filip Mladenović - ŽUTA OSA (8/24)
horheakimov - DUB PUB: Milion kvadrata
docsumann - Dokon um đavolje igralište
zilikaka - НАЦРТ РЕЗОЛУЦИЈЕ О ГЕНОЦИДУ У СРЕБРЕНИЦИ
Filip Mladenović - DUB PUB: A Bright New Day Is Coming
docsumann - Srbija u EU i NATO do 2030...
Filip Mladenović - DUB PUB: Woman, Hey
docsumann
Arhiva
Kategorije aktivne u poslednjih 7 dana
- Društvo (5)
- Život (4)
- Muzika (3)
- Gradjanske inicijative (3)
- Ljudska prava (2)
- Sport (2)
- Životni stil (2)
- Zdravlje (2)
- Zabava (2)
- Porodica (1)

